
![]()
![]()
![]()
![]()

 |
|
definition| derivation |graph | application|sample problems| links |
What is Logistic growth?
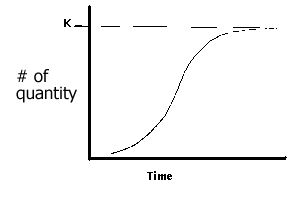
A logistic growth curve is an S-shaped (sigmoidal) curve that can be used to model functions that increase gradually at first, more rapidly in the middle growth period, and slowly at the end, leveling off at a maximum value after some period of time.
In 1838, the Belgian Pierre-Francois Verhulst suggested a revised model which
would eliminate the undesirable effect of unlimited growth from the exponential
model..
![]() which is the same as
which is the same as![]()
| r | birthrate of the population, under optimal conditions |
| K | carrying capacity-the level of the population that can be sustained by the given environment. |
| m | mortality constant |
Sometimes it can be helpful to think
of the equation in this form:
![]()
| Value of y | 0 | 0<y<K | K | y>K |
| 0 | + | 0 | - |
We notice that y decreases and thus the slope of the tangent lines to be drawn is negative whenever y>K but that whenever 0<y<K, the slopes are positive, and y increases.
Analysis
of the logistic growth curve:
The initial part of the curve is exponential; the rate of growth accelerates
as it approaches the midpoint of the curve. At the midpoint (K/2), the growth
rate begins to decelerate but continues to grow until it reaches an asymptote,
K which is called the "Carrying Capacity" for the environment.
Population growth, spreading of a rumor or virus,newton’s law of cooling
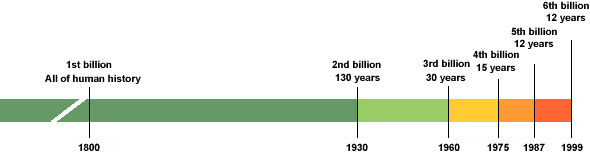
The logistic growth model is a more accurate representation of population growth becauseit takes into account that there are outside factors that may effect growth.
It is frequently used to model biological growth patterns where there is an initial exponential growth period followed by a leveling off as more of the population is infected or as the food supply or some other factor limits further growth.