|
|
|
What is Exponential growth?
Exponential growth assumes a quantity grows at rate propotional to what is already there.
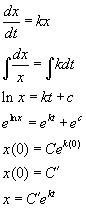
Basic concepts:
, then rate of change y is proportional to y,
then 
y0 |
Intial y value |
k |
constant If k>0, then k is a growth constant If k<0, then k is a decay constant |
Can use for radioactive decay, interest on money, population growth
However, the exponential growth model assumes unlimited growth. Only realistic for short period of time.
For example,population growth has become more complex and growth can no longer be considered truly exponential. The issues of the 21st Century are aging, the baby boom, urbanization, technological and medical advances, plus the socio-economic-political consequences, and pressures on resources and the environment.
There are several variations of this story...but these are my favorites...
A beggar came to a king's palace with an unsusual request. Instead of tasking for a meal, the beggar humbly requested a grain of rice for the first day, two on the second, four on the third day and so on - doubling the previous days contribution.
The next day the beggar came to claim his grain of rice. The townsfolk laughed at the beggar and said that he should have taken the king's kind offer for a full meal instead of the measly grain of rice. On the second day he was back for the two grains. A week later, he brought a teaspoon for the 128 grains that was due to him. In two weeks it was a non-negligible amount of half a kilo. At the end of the month it had grown to a whopping 35 tons. A few days later the king had to declare bankruptcy. That is how long it was needed to bring down the kingdom.
A variation is that beggar requested a one grain for the first square on a chess board, two for the second square and so on for each square. The king would be bankrupt long before the beggar got to the sixty-fourth square on the chess board.